Le but de ce projet est de convertir une imprimante 3D en machine capable de dessiner avec un stylo. Par la suite, à l’aide d’un modèle d’IA qui génère de l’écriture manuscrite, on va faire en sorte que l’imprimante puisse écrire une écriture manuscrite avec un stylo à bille à partir d’un texte informatique en entrée.
L’imprimante que j’ai récupérée est une A20 de ‘Geeetch’ :

J’ai commencé par démonter l’imprimante pour analyser son fonctionnement. Je ne voulais pas utiliser le software (logiciel) intégré pour contrôler les moteurs, mais bien mon propre programme, pour plusieurs raisons :
- La vitesse d’écriture ne sera pas limitée, car le software intégré limite la vitesse à cause du filament de plastique qui sort normalement de la buse.
- Cela me permet, au final, une utilisation plus simple. Il me suffirait d’envoyer ce que je veux écrire, sans convertir le fichier texte en 3D, ni me soucier des réglages de température, etc.
Pour ce faire, j’ai donc pensé utiliser un Raspberry Pi 4B (une petite carte électronique contrôlable) et un programme en Python (langage qui permet d’écrire un logiciel informatique), car c’est un langage que je maîtrise déjà.
Je vais donc présenter, sur ce site, le projet dans ses détails techniques, au jour le jour.
Jour 1 :
Ce jour-là, j’ai démonté l’imprimante pour comprendre son fonctionnement. J’ai donc compris plusieurs choses :
- Les moteurs de l’imprimante sont ce que l’on appelle des « stepper motors », mais l’on reverra cela plus tard.
- La carte mère semble avoir des petits « driver » pour les moteurs, mais je ne sais pas encore s’ils sont utilisables par le Rasp 4 (= Raspberry Pi 4). Voir l’image ci-dessous :

Jour 2 :
Il se trouve que les « drivers » présumés en sont bel et bien, ce sont des A4988, une puce de contrôle pour stepper motor bien connue.
Après quelques recherches, j’ai pu trouver les schémas suivants et donc être sûr que le Rasp 4 pouvait contrôler la puce.
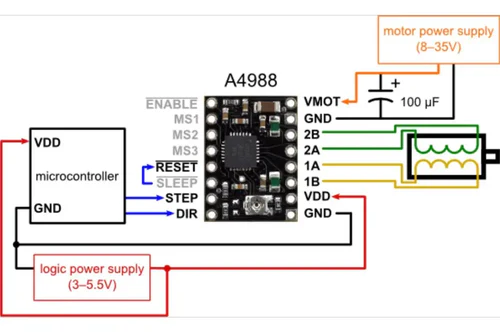
Mais il restait à savoir comment la relier, car je n’avais encore jamais utilisé mon Rasp 4 pour ce genre d’utilisation. Quelques recherches sur YouTube m’ont emmené vers cette vidéo : https://youtu.be/LUbhPKBL_IU?si=PXohBqDyhRvteU2I
Et surtout, ce schéma :
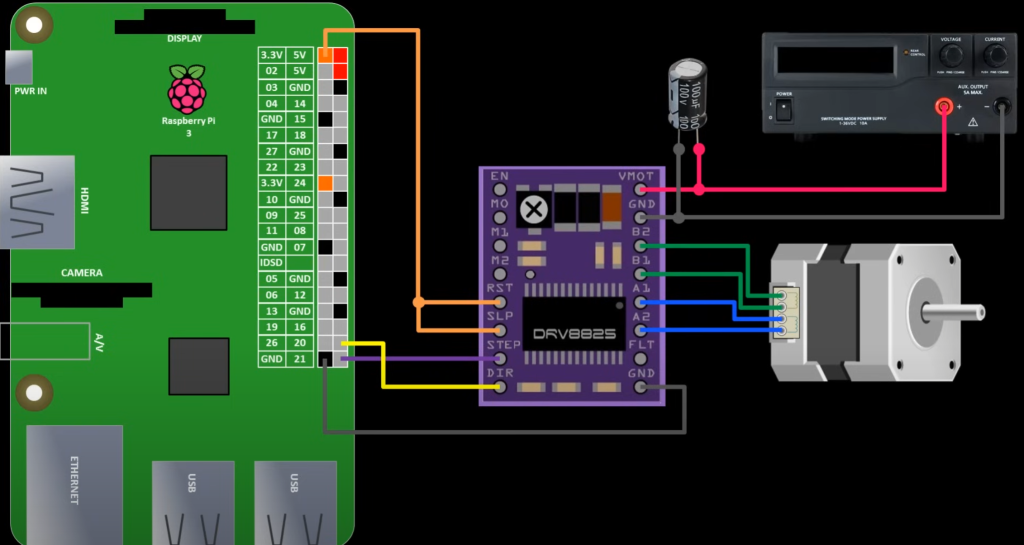
Mais, ça ne pouvait pas être si simple, évidemment. La seule vidéo qui parlait de contrôler un stepper motor avec un Rasp n’était pas avec la puce A4988, mais une DRV-8825 ici… Il se trouve donc que la manière de relier cette puce au Rasp 4 est différente de celle de la A4988.
Mais je me suis arrêté à ce point au jour 2.
Jour 3 :
Ce jour ci, j’ai pu a partir des deux schémas du jour 2 construire un schéma qui relie la A4988 au Rasp4 :
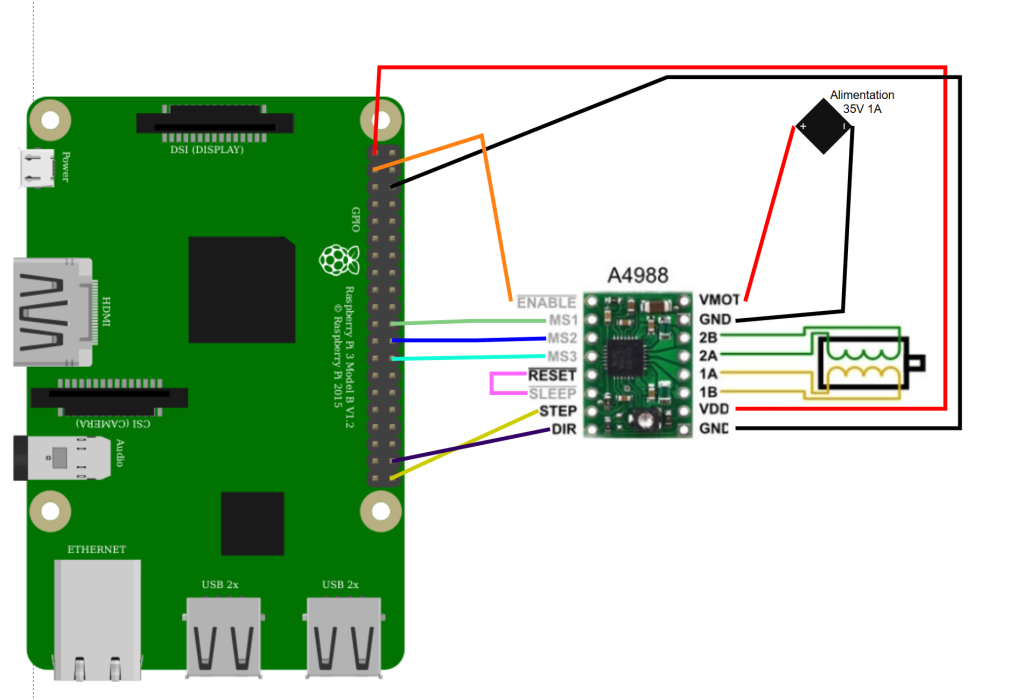
Bon, très bien, mais il faut maintenant coder le script qui va faire bouger le moteur, et le voici :
from time import sleep
import RPi.GPIO as GPIO
DIR = 20 # Direction GPIO Pin
STEP = 21 # Step GPIO Pin
CW = 1 # Clockwise Rotation
CCW = 0 # Counterclockwise Rotation
SPR = 200 # Steps per Revolution (360 / 1.8)
EN = 2 # Enable GPIO pin
GPIO.setmode(GPIO.BCM)
# Enable the board
GPIO.setup(EN, GPIO.OUT)
GPIO.output(EN, GPIO.LOW)
GPIO.setup(DIR, GPIO.OUT)
GPIO.setup(STEP, GPIO.OUT)
GPIO.output(DIR, CW)
MODE = (14, 15, 18) # Microstep Resolution GPIO Pins
GPIO.setup(MODE, GPIO.OUT)
RESOLUTION = {'Full': (0, 0, 0),
'Half': (1, 0, 0),
'1/4': (0, 1, 0),
'1/8': (1, 1, 0),
'1/16': (0, 0, 1),
'1/32': (1, 0, 1)}
GPIO.output(MODE, RESOLUTION['1/32'])
step_count = SPR * 32
delay = .005 / 32
for x in range(step_count):
GPIO.output(STEP, GPIO.HIGH)
sleep(delay)
GPIO.output(STEP, GPIO.LOW)
sleep(delay)
#Disable and cleanup
GPIO.output(EN, GPIO.HIGH)
GPIO.cleanup()Voici le résultat :
Maintenant, il est donc temps de comprendre ce qu’est un « stepper motor ».
Un stepper motor est un moteur qui, dans les détails, est assez complexe, mais plutôt facile à utiliser et à comprendre simplement. La base du stepper motor, vous l’aurez deviné, ce sont les « steps ». En fait, un stepper motor fonctionne « par step », contrairement à un simple moteur DC. Vous devez lui envoyer une pulsation pour que le moteur bouge d’un step (ici 1,8°, d’où « SPR = 200 » : un tour complet = 360°, donc en steps = 360 / 1,8 = 200).
Il faut aussi comprendre le « delay », qui est en fait le délai entre chaque pulsation du moteur. Plus il est faible, plus le moteur va vite, mais moins il a de torque (force). Il faut donc trouver un équilibre. Ici, 0.5 suffit pour les tests.
Il y a un dernier concept qui est très pratique : le « micro stepping ».
En fait, quand le moteur bouge de 1,8° par step, le mouvement est saccadé. On utilise donc le « micro stepping », qui permet de diviser l’angle par un certain nombre. Ici, on utilise 1/32. C’est donc pour cela que l’on multiplie le nombre de steps par tour complet (360 / (1,8 / 32) <=> (360 / 1,8) × 32) et aussi que l’on divise le delay (on fait 32 fois plus de steps dans le même temps).
Jour 4
Maintenant que nous pouvons faire bouger les moteurs, nous devons établir un « repère », simplement un système de coordonnées qui nous permet de placer un point n’importe où dans la zone de dessin. Ainsi, pour dessiner un cercle, on prend les coordonnées de chaque point et on y fait un point sur la feuille.
(Bien entendu, il est impossible de prendre tous les points du cercle, qui sont une infinité en réalité. Même avec un temps de 0,05 s par point, cela prendrait +∞ années pour tout le cercle — un peu trop long à mon goût. On choisit donc arbitrairement combien de points on prend, et cela introduit le principe de « résolution ».)
Pour ce faire, il nous faut tout d’abord placer les moteurs dans une position initiale. On pourrait le faire à la main, mais cela pose un problème de précision, et oublier cela avant de lancer le programme causerait une véritable catastrophe.
Mais le hasard (surtout le fait que le constructeur a eu le même souci que l’on tente de résoudre) a fait que l’imprimante est munie d’un « interrupteur de butée » :

Quand le moteur arrive en bout de course, on peut détecter cela grâce au fait qu’il appuie sur l’interrupteur.
Et pour éviter de réinventer la roue, on va s’en servir. Voici le plan :
1. On met tous les moteurs en butée.
2. On compte le nombre de steps à partir du zéro (la butée).
3. On garde en mémoire les coordonnées du moteur à tout moment.
4. Soient Cnow les coordonnées actuelles, Cnext les prochaines coordonnées où l’on veut se rendre, et Mv le mouvement en steps à effectuer. Pour chaque axe :
Mv = Cnext – Cnow
En effet, si Cnext < Cnow alors Mv < 0, donc le moteur recule, et vice versa.
5. On effectue Mv pour chaque axe ! (Sauf si Cnext est négatif, dans ce cas, aucun calcul ni mouvement n’est fait, par protection du moteur.)
Il est donc temps de connecter le Pi à l’interrupteur. Mes premières recherches m’ont mené à ce qu’on appelle une « résistance de pull-up » : un système qui permet de détecter si un interrupteur est ouvert ou fermé, sans avoir besoin d’envoyer du courant à travers. C’est une sorte de petite astuce électronique qui repose sur des comparaisons de tension grâce à des résistances.
Mais inutile de plonger dans les détails de cette magie noire… car si elle est mal maîtrisée, les conséquences peuvent être sérieuses. Par exemple : griller le pin n°12 de mon Rasp4. (Oui, c’est arrivé… vous vous en doutez.)
Jour 5 :
J’ai fini par récupérer un Rasp 3 (moins puissant, mais bien suffisant pour le projet). Cela m’évitera d’abîmer davantage du matériel coûteux sans que cela soit nécessaire.
Ajoutons donc, sur notre schéma, l’interrupteur :
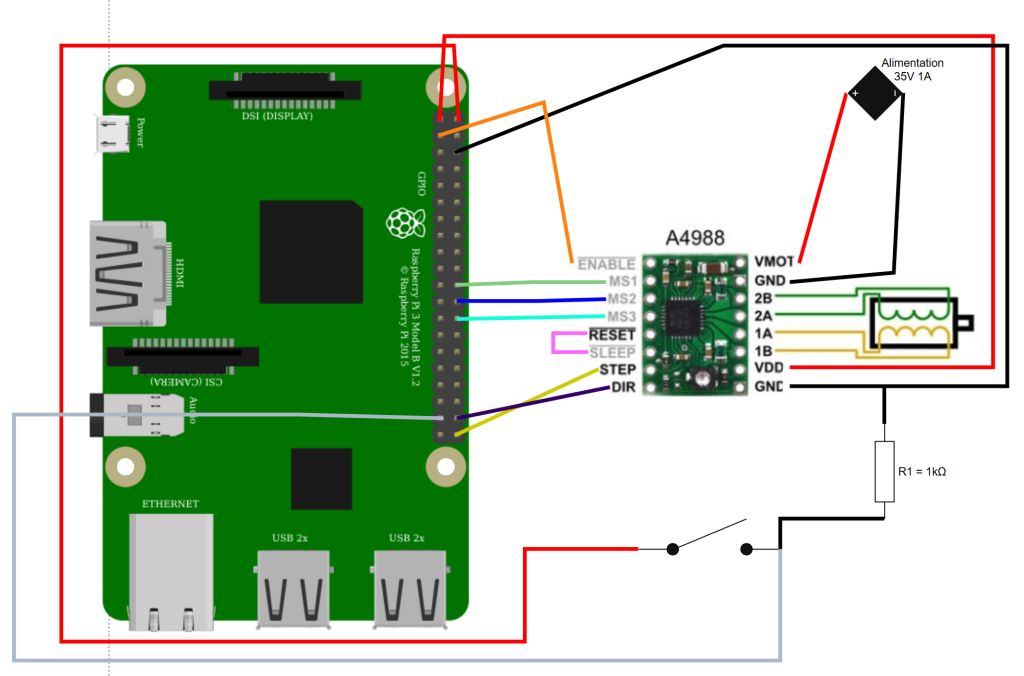
On relie donc l’entrée de l’interrupteur au pin 2 (sortie 5V), et la sortie au pin 37 et au GND en passant par une résistance de 1 kΩ. Mais pourquoi ?
Avant tout, il faut comprendre pourquoi on le relie au GND (ground = terre). Il faut savoir qu’il y a toujours des perturbations ambiantes, et que le pin du Rasp est très sensible. On relie donc tout ça au GND pour supprimer ces perturbations.
Mais sans la résistance R1, il y aurait un gros problème :
Calculons l’intensité I passant entre le pin 5V et le GND sans la résistance :I = R/U
I = 5/0
I = +∞A
Le Pi va donc envoyer l’intensité maximale, ce qui, au mieux, va juste causer un court-circuit, et au pire, peut faire surchauffer les câbles et donc provoquer un risque d’incendie.
donc on place une résistance, et :
I = 5/1000
I = 5*10^-3 A
Ce qui est déjà bien plus raisonnable.
Dans les faits, on devrait aussi en placer une avant le pin 37 du Pi pour le protéger. Je le ferai sûrement pour la version finale, mais pour le moment, je me remets à la résistance interne du Pi, qui suffit pour des tests courts.
J’ai donc adapté le code python, voici :
DIR = 20 # Direction GPIO Pin
STEP = 21 # Step GPIO Pin
CW = 1 # Clockwise Rotation
CCW = 0 # Counterclockwise Rotation
SPR = 200 # Steps per Revolution (360 / 1.8)
EN = 2 # Enable GPIO pin
SWITCH = 26
GPIO.setmode(GPIO.BCM)
# Enable the board
GPIO.setup(EN, GPIO.OUT)
GPIO.output(EN, GPIO.LOW)
# set the switch up
GPIO.setup(SWITCH, GPIO.in)
GPIO.setup(DIR, GPIO.OUT)
GPIO.setup(STEP, GPIO.OUT)
GPIO.output(DIR, CW)
MODE = (14, 15, 18) # Microstep Resolution GPIO Pins
GPIO.setup(MODE, GPIO.OUT)
RESOLUTION = {'Full': (0, 0, 0),
'Half': (1, 0, 0),
'1/4': (0, 1, 0),
'1/8': (1, 1, 0),
'1/16': (0, 0, 1),
'1/32': (1, 0, 1)}
GPIO.output(MODE, RESOLUTION['1/32'])
step_count = SPR * 32
delay = .005 / 32
For x in range(20) :
if GPIO.input(SWITCH) == GPIO.LOW :
GPIO.output(DIR, CW)
for x in range(step_count):
GPIO.output(STEP, GPIO.HIGH)
sleep(delay)
GPIO.output(STEP, GPIO.LOW)
sleep(delay)
elif GPIO.input(SWITCH) == GPIO.HIGH :
GPIO.output(DIR, CCW)
for x in range(3) :
for x in range(step_count):
GPIO.output(STEP, GPIO.HIGH)
sleep(delay)
GPIO.output(STEP, GPIO.LOW)
sleep(delay)
#Disable and cleanup
GPIO.output(EN, GPIO.HIGH)
GPIO.cleanup()Voici ce que cela donne :
<video>
Ce code permet d’approcher le moteur de la butée, puis de reculer 3 fois d’affilée après l’avoir atteinte, le tout en boucle 20 fois.
Jour 6
Maintenant que nous pouvons envoyer le moteur en butée, il nous faut établir le repère. Mais avant cela, je me suis permis de coder une petite librairie Python simple, qui inclut les fonctions de base des moteurs. En voici quelques-unes :
Les fonctions high() et down(), qui permettent de faire tourner le moteur dans les deux directions :
def high(self, step : int):
if self.is_setup == 0:
print("This mottor wasn't setup.")
return print("Aborting the program !")
GPIO.output(self.DIR, 1)
print(f"The motor {self} is going up for {step} 1/16 steps.")
for i in range(step):
GPIO.output(self.STEP, GPIO.HIGH)
sleep(delay)
GPIO.output(self.STEP, GPIO.LOW)
sleep(delay)
def down(self, step : int) :
if self.is_setup == 0:
print("This mottor wasn't setup.")
return print("Aborting the program !")
GPIO.output(self.DIR, 0)
print(f"The motor {self} is going down for {step} 1/16 steps.")
for i in range(step):
GPIO.output(self.STEP, GPIO.HIGH)
sleep(delay)
GPIO.output(self.STEP, GPIO.LOW)
sleep(delay)Si vous voulez voir tout le code, vous le trouverez ici : see code on github
Mais la plus importante de toute est bien la fonction reset, car elle permet de renvoyer le moteur en butée
def reset(self):
if self.is_setup == 0:
print("This mottor wasn't setup.")
return print("Aborting the program !")
print("Seting the motor to 0 on the axis.")
GPIO.output(self.DIR, 1)
while True :
if GPIO.input(self.SWITCH) == 1 :
return print("The motor was reset !")
elif GPIO.input(self.SWITCH) == 0 :
GPIO.output(self.STEP, GPIO.HIGH)
sleep(delay)
GPIO.output(self.STEP, GPIO.LOW)
sleep(delay)Pour comprendre ce code, il faut déjà savoir que je vous ai menti. En effet, le code présenté plus tôt au jour 5 n’est pas vraiment fait pour renvoyer le moteur en butée. Je m’explique :
Au jour 5, le code envoyait le moteur vers la butée, jusqu’à ce qu’il détecte que l’interrupteur correspondant soit fermé. Dans ce cas, il renvoyait le moteur dans l’autre sens quelques instants, puis il recommençait le tout. On pourrait se dire que cela fonctionne, mais les interrupteurs ne sont pas parfaits, et l’isolation non plus. Le pin du Rasp étant très sensible, il est capable de détecter une impulsion de l’ordre d’une μs (microseconde), et dans ce cas, il renvoyait tout de suite le moteur. Il était alors assez fréquent que le moteur n’arrive pas jusqu’à la butée, surtout quand plusieurs moteurs étaient en action en même temps. Le problème est donc que le moteur pourrait s’arrêter au milieu du plateau et penser qu’il est en butée, ce qui pourrait endommager tout le système.
C’est alors qu’a commencé une longue période de recherches pour résoudre ce problème. J’ai d’abord tenté d’isoler davantage les câbles, mais en vain. J’ai donc fini par opter pour une solution logicielle assez simple :
while True :
print(GPIO.input(self.SWITCH))
if GPIO.input(self.SWITCH) == 1 :
sleep(0.2)
if GPIO.input(self.SWITCH) == 0 :
pass
elif GPIO.input(self.SWITCH) == 1:
return print(f"The motor {self.name} was set to 0 on the main axis !")
elif GPIO.input(self.SWITCH) == 0 :
GPIO.output(self.STEP, GPIO.HIGH)
sleep(delay)
GPIO.output(self.STEP, GPIO.LOW)
sleep(delay)Ce code se traduit par
Si l'interrupteur est activé :
attendre 2 sec
si l'interrupteur est désactivé :
recommencer
sinon :
le moteur est en butée
sinon :
envoyer le moteur vers la butée
La différence est donc que l’on attend un peu, et on regarde si l’interrupteur est toujours désactivé. La probabilité d’avoir deux perturbations à ces deux moments précis est tellement faible qu’on la considère comme impossible.
Le code final est donc :
def reset(self):
if self.is_setup == 0:
print("This mottor wasn't setup.")
return print("Aborting the program !")
print(f"Setting the motor {self.name} to 0 on the main axis.")
GPIO.output(self.DIR, self.dir_down)
while True :
print(GPIO.input(self.SWITCH))
if GPIO.input(self.SWITCH) == 1 :
sleep(0.2)
if GPIO.input(self.SWITCH) == 0 :
pass
elif GPIO.input(self.SWITCH) == 1:
return print(f"The motor {self.name} was set to 0 on the main axis !")
elif GPIO.input(self.SWITCH) == 0 :
GPIO.output(self.STEP, GPIO.HIGH)
sleep(delay)
GPIO.output(self.STEP, GPIO.LOW)
sleep(delay)De plus, je doit vous avouer autre chose, durant mes recherches j’ai fini par lire la documentation officiel de ma puce de contrôle pour les moteurs, et la partie sur le micro steping a attiré mon attention :
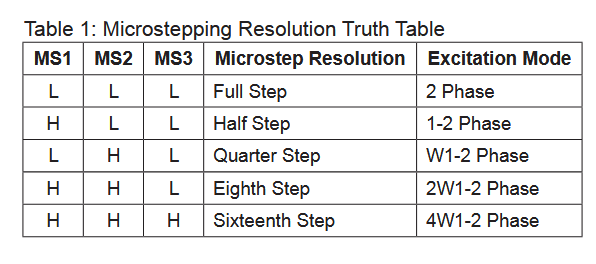
Les plus attentifs d’entre vous l’auront vu. Pour rappel, je pense avoir mis ma puce en mode 1/32 step, le problème est que ce mode n’existe en fait pas sur ma puce…
En fait, le tuto que j’ai trouvé utilisait une puce qui n’avait vraiment rien à voir avec la mienne et, étant trop flemmard pour lire la documentation, j’ai fait confiance au tuto.
Cela n’est pas très grave, mais ça veut aussi dire que depuis le début, ma puce fonctionnait en mode full step, et donc avec les mouvements les plus saccadés qui soient. Mais cela n’a posé aucun souci… pour l’instant, je vais me contenter de cela.
Jour 7
Je tient a dire que le projet dure en réalité depuis un mois, mais, je n’ai pas le temps de travailler dessus tous les jours, loin de là, parfois même pas un jours entier par semaines.
À partir de ce moment, une grosse période de code commence. Je ne vais pas passer en détail sur tout ce qu’il s’est passé, je vous invite à regarder le GitHub pour cela. Mais j’ai codé une deuxième partie à ma librairie, la partie “Stylus” (stylo ou stylet). Cette partie est celle qui permet de prendre les trois moteurs, de les combiner, de les mettre en butée et de créer un système de coordonnées avec.
La partie Stylus était assez simple : on doit d’abord définir les trois moteurs, les setup, ce qui active des éléments cruciaux comme l’interrupteur ou autre.
Quand nous avons nos trois moteurs, il ne nous reste plus qu’à créer un Stylus, ici appelé “Main_stylus”. Voici à quoi ce procédé ressemble :
Y_motor = Motor(Y_motor_info, "Y_motor", 0, 1)
Y_motor.setup()
X_motor = Motor(X_motor_info, "X_motor", 0, 1)
X_motor.setup()
Z_motor = Motor(Z_motor_info, "Z_motor", 0, 1)
Z_motor.setup()
Main_stylus = Stylus([2599, 2543, 6530])
Main_stylus.add_motor(Y_motor, "Y")
Main_stylus.add_motor(X_motor, "X")
Main_stylus.add_motor(Z_motor, "Z")
Main_stylus.setup()Nous allons maintenant nous attarder sur la dernière ligne de code, Main_stylus.setup().
C’est cette fonction qui va créer le repère orthogonal* dont nous avons besoin. Elle va d’abord utiliser la fonction reset de chaque moteur, puis, par la suite, définir la variable coordinate = [0, 0, 0].
Les coordonnées de départ sont à 0 pour chaque axe, car tous les moteurs sont remis à 0.
On remarque aussi que lorsque je définis le Stylus, j’y mets des chiffres :Main_stylus = Stylus([2599, 2543, 6530])
C’est en fait le maximum pour chaque axe. Il est calculé en mettant manuellement le moteur au maximum, puis en comptant le nombre de steps pour revenir en butée.
*Pourquoi un repère Orthogonal ?
Avant tout, qu’est ce qu’un repère Orthogonal, c’est un repère ou les axes sont perpendiculaire les uns des autres, comme ceci :
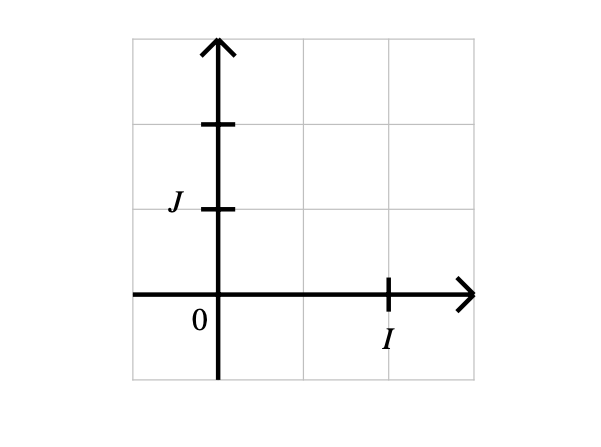
Mais la particularité, c’est que les distance entre les graduations de chaque axe ne sont pas les même, cela est le cas ici, car un step sur le moteur Y ne fait pas la même distance que sur le moteur X, cette différence se joue au micro mètre, elle n’est donc pas significative, je ne me prend pas la tête avec dans le code.
Jour 8
Maintenant que j’ai une base solide, il est temps de brancher tous les moteurs pour commencer les tests, voici le setup:

Et le schéma (attention les yeux) :
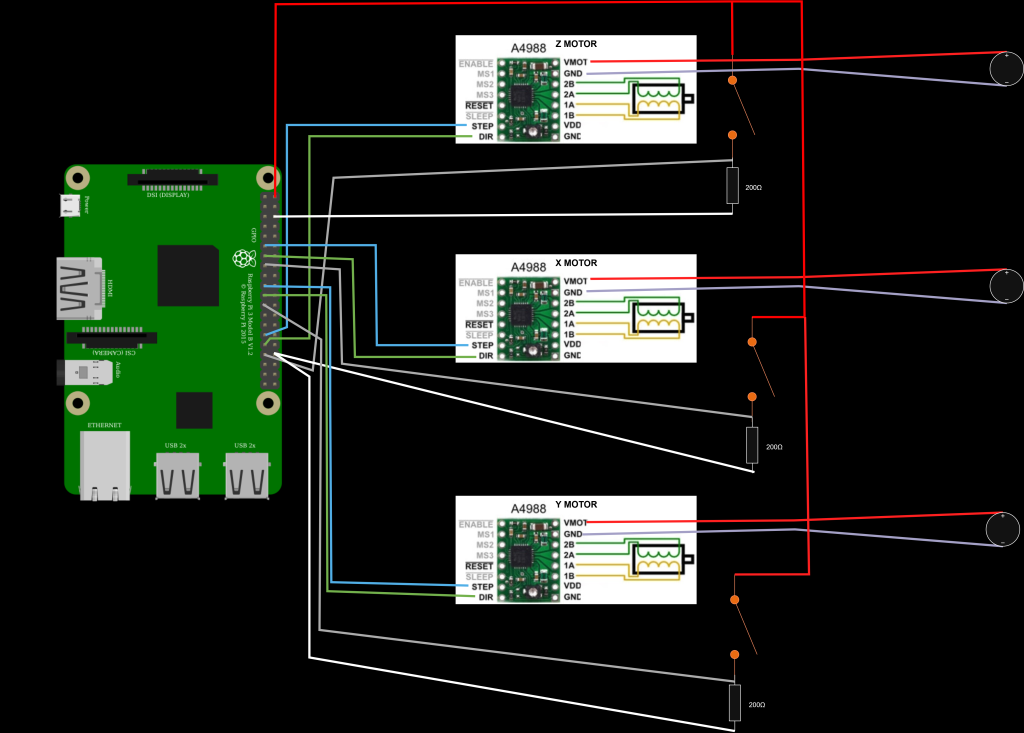
*Les pin VDD et GND sont respectivement connectés au 5V et GND du Pi, ce n’est juste pas afficher sur le schéma.
On remarque déjà plusieurs nouveautés. Avant tout, les pins MS1-3, qui permettent le micro-stepping, ne sont plus connectés. En effet, il n’est pour le moment pas utile de l’activer (peut-être dans le futur pour des mouvements plus fluides).
De plus, les résistances sont passées de 1 kΩ à 220 Ω, car il se trouve que 220 est une norme pour les résistances dans ce genre d’utilisation. Cela permet d’éviter de prendre de faux signaux (la résistance pour aller au GND et non au pin est réduite).
On peut maintenant passer au mouvement des moteurs dans le repère, pour l’instant, nous allons faire des mouvements moteur par moteur, c’est à dire que nous ne déplacerons pas la buse en diagonal.
voici le code de la fonction go_to() qui permet de mettre la buse en une coordonnées [x, y, z]:
def go_to(self, next_coordinate : list):
motor_list = [self.X_motor, self.Y_motor, self.Z_motor]
#cannot move if the stylus isn't setup :
if self.coordinate == None :
return print("Error, the stylus wasn't setup yet.")
for i in range(len(self.co_list)) :
if next_coordinate[i] == -1 :
pass
elif next_coordinate[i] - self.coordinate[i] != 0 and i == None :
return print(f"Error, you tried to move an axis wich coresponding motor wasn't setup! Please setup the {self.co_list[i]} motor.")
elif next_coordinate[i] > self.max[i] or next_coordinate[i] < 0 :
return print(f"Error, you tried to reach a coordinate that is out of reach! The max for the {self.co_list[i]} axis is {self.max[i]} and min is 0, you tried {next_coordinate[i]}")
elif next_coordinate[i] != self.coordinate[i] :
mouvement = next_coordinate[i] - self.coordinate[i]
self.move_axis(i, mouvement)Expliquons ce code simplement. En premier lieu, nous regardons les coordonnées une par une. Ce code va donc être exécuté trois fois, car nous sommes en 3D (même si, dans les faits, la coordonnée Z ne sera que très peu utilisée).
La première chose que nous faisons, c’est regarder les coordonnées entrées. Elles sont sous la forme d’une liste : [456, 789, 987] par exemple. Il est à noter que la coordonnée -1 a un effet spécial : elle permet de ne pas bouger l’axe. Cela est plus optimisé que de simplement mettre la coordonnée actuelle d’un axe comme destination, car dans ce cas, le programme calculerait quand même le mouvement du moteur, qui serait bien entendu nul.
Ensuite, nous vérifions si la coordonnée demandée est au-dessus du maximum, ou si elle est inférieure à -1 (auquel cas, le moteur ne peut pas reculer plus loin que 0).
Si toutes les vérifications sont passées, nous allons définir le mouvement avec la formule définie au jour 4 (Mv = Cnext - Cnow). Nous faisons ensuite effectuer ce mouvement au moteur qui correspond à l’axe, grâce à la fonction move_axis().
Tout cela, répété 3 fois, permet de se déplacer sur le repère facilement.
Voici ce que cela donne :
Jour 9
Cela fait déjà un bon moment que j’ai entamé ce projet, et j’arrive enfin au stade où je peux tracer de véritables formes, en commençant par les diagonales !
Mais pourquoi les diagonales ? Parce que lorsqu’on sait tracer une courbe et une diagonale, on peut pratiquement tout dessiner… et la diagonale reste bien plus simple à réaliser qu’une courbe.
Maintenant, comment fait-on pour tracer cette diagonale ? Ma première intuition serait de bouger les moteurs X et Y en même temps, avec une vitesse différente ; j’ai donc d’abord approché l’idée du code asynchrone.
Le code asynchrone est une méthode originellement utilisée pour l’optimisation, laissez-moi vous expliquer simplement :
Quand vous lancez votre programme informatique, sans aucune optimisation (rare dans les programmes de nos jours), le programme va exécuter les lignes de code dans l’ordre exact où elles sont écrites (plus ou moins, car il peut retourner en arrière pour reprendre des bouts de code). Mais ce qui est important à retenir, c’est que le code normal est une simple autoroute, et le seul moyen d’accéder à chaque étape, c’est de passer par cette autoroute.
Maintenant, que se passe-t-il si l’autoroute est bouchée ? Le programme “lag”, il est lent et peut même crasher dans certains cas. Une des nombreuses techniques d’optimisation dans ce cas est le code asynchrone. Prenons un programme simple : il va créer une page web avec les infos de tous les retards de vol annoncés dans 5 des plus grands aéroports mondiaux. Pour ce faire, il va aller chercher sur les sites tous les retards et les mettre sur une page web. Le problème est que les sites sont longs à répondre, et ce temps est donc multiplié par le nombre de sites. Nous allons donc mettre chaque bout de code pour les 5 sites dans 5 fonctions asynchrones différentes. Quand nous allons lancer ces fonctions, elles vont s’exécuter en parallèle, et donc finir plus ou moins en même temps pour les 5.
Ce que nous voyons, c’est que le code asynchrone est comme une nationale que l’on peut emprunter si l’autoroute est bouchée. Elle est un peu moins rapide, car l’ordinateur est partagé entre plusieurs tâches en même temps, mais si on lance chaque tâche sur une nationale, l’autoroute ne sera pas bouchée et le programme mettra au final moins de temps à s’exécuter.
Ce qui nous intéresse ici, c’est que deux morceaux de code peuvent s’exécuter en parallèle, j’ai donc essayer de simplement trace un diagonal a un angle de 45°, car étant la moitié de 90°, il suffit donc de faire bouger les deux moteur a la même vitesse sur la même durée.
Après avoir codé ce qu’il fallait pendant quelques jours, j’ai été surpris de voir que les moteurs ne bougeaient qu’un par un, même si le code était bien asynchrone. J’ai alors fait des recherches, et il se trouve que pour que le code asynchrone s’exécute en parallèle, il faut que ce qu’il y est écrit soit compatible, et évidemment, la librairie qui permet de communiquer aux pins du Rasp4 était incompatible.
C’est alors que je me penche sur le multithreading. Ici, on ne simule plus du code en parallèle, mais on utilise une fonctionnalité physique du processeur pour exécuter plusieurs petit bout de programmes a part les un des autres, plus besoin de se soucier de compatibilité, mais nous serons par contre limité par le nombres de thead physique (inchangeable).
Mais, durant mes recherches, je me suis rendu compte que cela poserait pas mal de problèmes :
- Si les mouvements ne sont pas lancés exactement au même moment, la diagonale sera complètement à côté de ce qu’elle devrait être.
- Si, durant le mouvement, un des deux morceaux de code met un peu plus de temps à s’exécuter que normalement, le deuxième ne l’attendra pas, et donc tout finira décalé.
Alors, comment est-ce que l’on fait cela ?
Eh bien, la réponse est en fait sous vos yeux (en quelque sorte). Imaginons que nous ayons un écran, c’est-à-dire une grille de pixels. On peut soit allumer un pixel, soit l’éteindre, mais pas à moitié : soit totalement ON, soit totalement OFF.
Maintenant, imaginons que sur cet écran, on veuille tracer une diagonale qui ne passe pas totalement par un pixel, exemple :
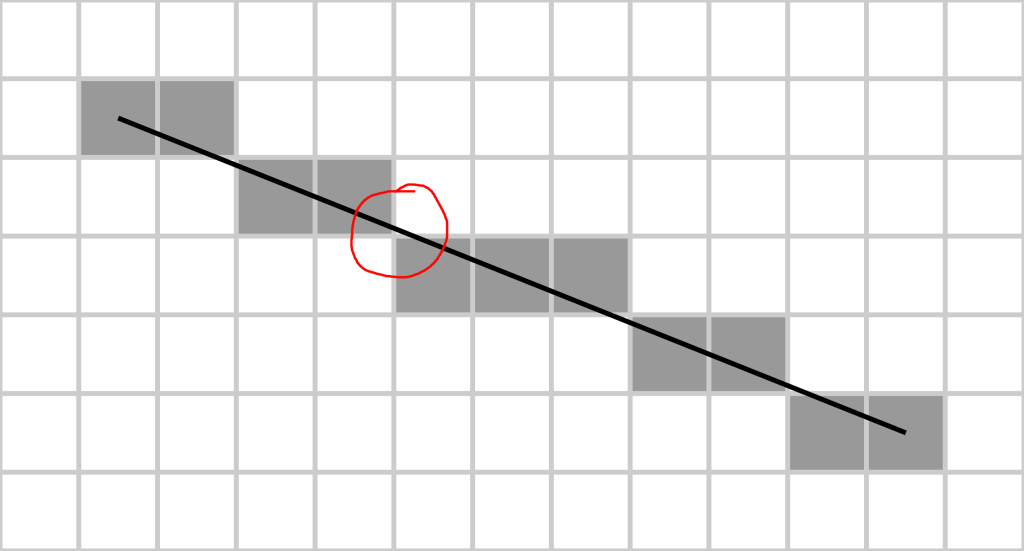
Comment sait-on si l’on doit monter d’un pixel ou pas ? Prenez l’endroit entouré en rouge : comment le programme sait-il qu’il doit faire monter le prochain pixel ?
Cette question, un certain Bresenham se l’est posée bien avant moi, et il a créé “l’algorithme de tracé de segment de Bresenham“, il était, et ses bases le sont toujours, utilisé dans les systèmes d’affichage sur écran dans un peu près tout les ordinateurs (et donc smartphones, télévisions etc..) . Il se trouve que si l’on fait monter le moteur Y quand le pixel monte, et avancer le moteur X quand le pixel se décale, on arrive à tracer des diagonales !
L’approche finale est donc step by step, c’est-à-dire que l’on bouge chaque moteur un par un. Cela nous donne un très bon contrôle de la forme finale, sans problème de synchronisation, et surtout, les moteurs bougent à une fréquence tellement rapide que l’on ne voit pas que le mouvement est en réalité saccadé.
Voici l’algorithme écrit en python:
#use the bresenham algorithm to get all the pos of the x and y axis
# define everything we need
coordinate_by_step = []
x0, y0 = starting
x1, y1 = end
dx = abs(x1 - x0)
dy = abs(y1 - y0)
sx = 1 if x1 >= x0 else -1
sy = 1 if y1 >= y0 else -1
if dx > dy:
err = dx // 2
while x0 != x1:
coordinate_by_step.append([x0, y0])
print([x0, y0])
err -= dy
if err < 0:
y0 += sy
err += dx
x0 += sx
else:
err = dy // 2
while y0 != y1:
coordinate_by_step.append([x0, y0])
print([x0, y0])
err -= dx
if err < 0:
x0 += sx
err += dy
y0 += sy
coordinate_by_step.append([x1, y1])
print("All value have been processed")Je n’irai pas dans les détails de comment marche ce code ici, mais si vous êtes curieux, vous pouvez lire la page Wikipédia : https://fr.wikipedia.org/wiki/Algorithme_de_trac%C3%A9_de_segment_de_Bresenham
Mais pour faire simple : à chaque étape, on augmente la coordonnée “dominante” (celle qui va toujours augmenter, elle varie selon la direction de la ligne) et ensuite, on regarde si la courbe s’éloigne trop du pixel en question. Si oui, on monte d’un sur l’autre axe.
Note; dans le cas ou la ligne est dirigé vers le bas, on a juste a prendre l’opposé de chaque mouvement calculé par l’algorithme classique.
Voici une petite tentative à la main, car j’avais une flemme pas possible de mettre en place un système de tracé graphique en Python :
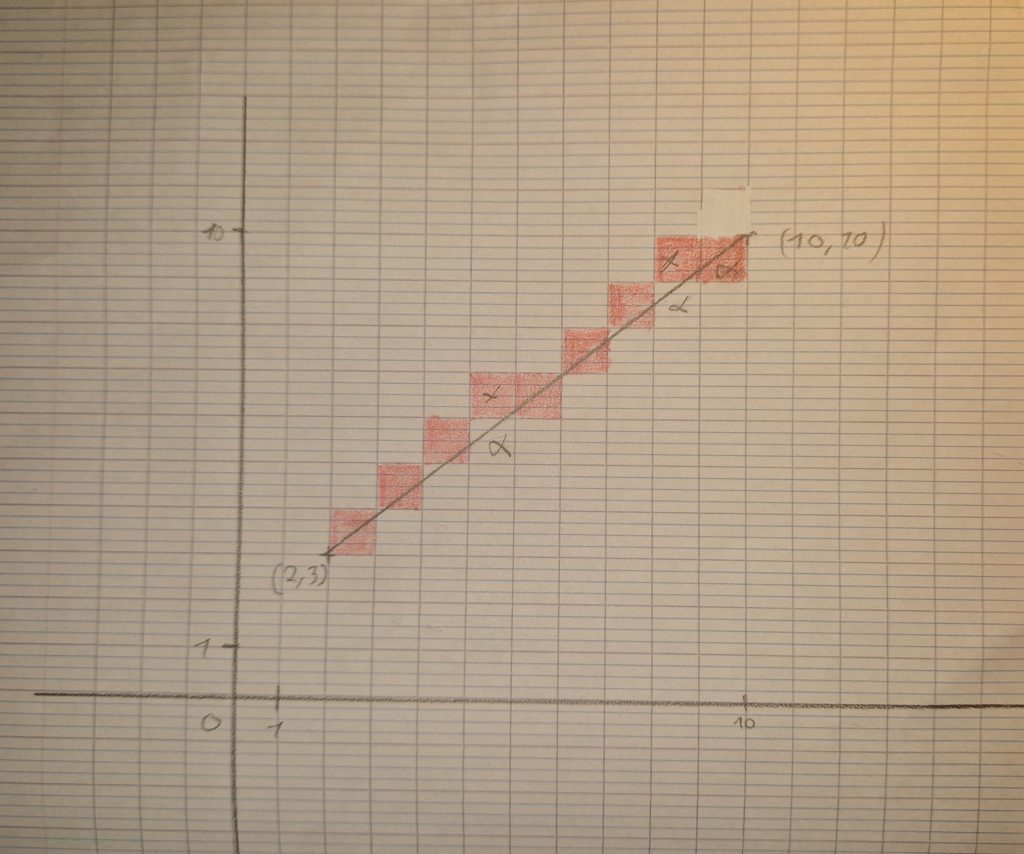
Il ne me reste plus qu’a intégrer cela à mon programme !
Voici la fonction que j’ai créé pour cela :
def line(self, starting : list[int, int], end : list[int, int]):
#first put the pen up
self.up()
#check if the max isn't exceded
if end[0] > self.max[0]:
self.down()
return print(f"Sorry, but the given point is outside of the limit for the X axis, you gaved {end[0]} and the max is {self.max[0]}")
if end[1] > self.max[1]:
self.down()
return print(f"Sorry, but the given point is outside of the limit for the Y axis, you gaved {end[1]} and the max is {self.max[1]}")
print("Starting the processing of the value with the bresenham algorithm")
#use the bresenham algorithm to get all the pos of the x and y axis
# define everything we need
coordinate_by_step = []
x0, y0 = starting
x1, y1 = end
dx = abs(x1 - x0)
dy = abs(y1 - y0)
sx = 1 if x1 >= x0 else -1
sy = 1 if y1 >= y0 else -1
if dx > dy:
err = dx // 2
while x0 != x1:
coordinate_by_step.append([x0, y0])
print([x0, y0])
err -= dy
if err < 0:
y0 += sy
err += dx
x0 += sx
else:
err = dy // 2
while y0 != y1:
coordinate_by_step.append([x0, y0])
print([x0, y0])
err -= dx
if err < 0:
x0 += sx
err += dy
y0 += sy
coordinate_by_step.append([x1, y1])
print("All value have been processed")
#get to the starting point
self.go_to([starting[0], starting[1], -1])
self.down()
#remove the first coordinate since we already got there
coordinate_by_step.__delitem__(0)
print("Processing the movement based on the value")
mov_by_step = []
last_co = [starting[0], starting[1]]
for coordinate in coordinate_by_step :
mov = [coordinate[0]-last_co[0], coordinate[1]-last_co[1]]
print(mov)
mov_by_step.append(mov)
last_co = coordinate
#Now, we do the movement for each axis and each step
for mov in mov_by_step:
self.move_axis(0, mov[0])
self.move_axis(1, mov[1])
#Now, actualise the coordinates
self.coordinate[0] = end[0]
self.coordinate[1] = end[1]
#at the end, we put the pen up again, and print the result.
self.up()
return print("The line was drawn sucessfully !")Nous allons donc résumer simplement cette fonction:
En premier lieu, nous utilisons la fonction Stylus.up() pour monter l’axe Z (et donc le crayon) de quelques mm au-dessus de la feuille. Ensuite, après quelques vérifications, c’est là que toute la magie commence !
Nous allons lancer l’algorithme de Bresenham et calculer les coordonnées de chaque point (avec une résolution de 1 step). Quand le tout est fini, nous allons stocker les valeurs dans une liste. Avant de passer à la suite, nous allons déplacer les moteurs au début de la ligne et retirer cette coordonnée de la liste puisque nous y sommes déjà.
Après cela, nous allons ouvrir cette liste et, à l’aide de la formule pour convertir des coordonnées en mouvements, énoncée à de nombreuses reprises, nous allons transformer cette liste en une suite de mouvements que les moteurs peuvent comprendre.
Quand les deux étapes précédentes sont exécutées, nous allons pouvoir utiliser la fonctionself.move_axis() sur l’axe X et Y avec tous les mouvements à la suite.
Note : nous utilisons ici la fonction move_axis() et non pas go_to(). Même si cela éviterait d’avoir deux lignes de code qui se ressemblent beaucoup, cela ajouterai en fait plein de calculs inutiles qui rendent le tout plus lent.
De plus, il est important de savoir pourquoi nous calculons tout avant de faire bouger les moteurs. Car au final, que l’on calcule le mouvement entre chaque action des moteurs ou avant, le temps final est le même. Sauf que, avant tout, c’est plus beau de voir un mouvement fluide et non saccadé par les calculs. Et surtout, il faut se dire que rien ne nous empêche de prendre la liste de mouvements dans un fichier. Là où, si les calculs étaient dynamiques durant tout le code, il faudrait apporter plein de modifications pour que cela soit possible. Or, quand nous aurons des mouvements de plusieurs centaines de milliers de steps à calculer, il sera préférable de faire les calculs sur un ordinateur plus puissant et de transférer le tout dans un fichier. D’où l’intérêt de commencer dès maintenant à rendre le code compatible avec ce mode de fonctionnement.
Mais assez parler comme ça, voici le résultat !
One response to “Projet : Victor Hugo”
-
Salut,
Je trouve que ça devient de plus en plus compliqué, et pour arriver a écrire tout l’alphabet, ça va être une sacrée galère.
Sauf erreur, pour chaque lettre, chaque signe ou symbole il va falloir écrire un code . Si les caractères sont dessinés comme écrits a la main, et ne sont pas des caractères d’imprimerie ça va être encore plus dur!!
Bon courage pour la suite !!!
Leave a Reply